Definition
The complex plane and the fractal’s iterative equation.
The Mandelbrot set is a fractal, or self-similar pattern, defined as, “the set for complex numbers c for which the function f(z) = z^2 + c does not diverge when iterated from z = 0.” However, this formal and mathematical description says almost nothing about it and can be confusing to those new to the subject. In this post, I will be attempting to break down this definition and explain the math behind it.
Complex Numbers
What are they and how do they relate to the set?

To start off, a complex number is any number which can be expressed as the sum of a “real” and “imaginary” part. This is usually expressed in the form a + bi, where a and b are real numbers, like those on the standard number line, and i is the imaginary unit. This “imaginary” number i is equal to the square root of -1. The imaginary unit, along with all other purely imaginary numbers, lie along the imaginary axis, perpendicular to the real axis, forming what is known as the complex plane. This is quite similar to the Cartesian plane, but the x-axis is replaced with the real axis, and the y-axis with the imaginary axis. All complex numbers reside on this plane, including purely real and imaginary numbers. Past the complex plane, the Cayley–Dickson construction can be used to derive the algebra for hypercomplex numbers, such as quaternions and octonions, but this is beyond the scope of this article.
The Fractal’s Equation
How does it work and why does it produce the fractal?
The function behind the Mandelbrot set says that for any complex input, z, the output is z^2 + c, where c is a number in the complex plane. This function does not behave as one might expect, though, since it does not strictly apply to real numbers. More on this can be read here.

To produce the fractal, a number c must be iterated through the equation, meaning it is repeatedly plugged into the equation, where the output becomes the input for the next iteration. A complex number c is part of the set if it does not grow to infinity when iterated an infinite number of times. These points are represented by the color black in the image below. The colors denote the number of iterations it takes for a point to surpass a finite threshold radius from the origin (how fast the numbers “blow up”). In the images, every pixel has a corresponding number on the complex plane.

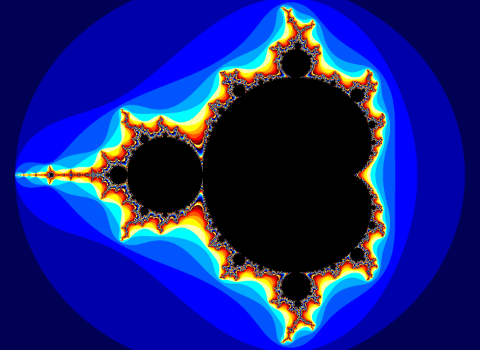
Interesting Properties
What makes it unique and worth studying?
- The Fractal is bounded, meaning it is finite in size or area, although its perimeter is infinite. This also implies that the whole fractal can be contained in circle of finite radius from the origin.
- The Mandelbrot set exists between the interval [-2, 1/4] on the real axis and is also symmetric about it.
- There is an infinite number of “minibrots,” or smaller versions of the whole fractal within it.
- The fractal “dimension” of the edge is 2. This means it equivalent to an area, despite being a curve.
- The “antennas” of the bulbs follow the Fibonacci sequence. Further explanation for this can be found here.
- Julia sets using a point within the Mandelbrot set are “solid” while those using points not contained in the set are “disconnected,” so to speak. An explanation for this can be found here.
- The whole set is “connected.”
Mandelbrot Zoom
This is one of the deepest “zooms” I could find

Pingback: Julia Sets | Science and Code
Pingback: Julia and Mandelbrot Set Explorer | Science and Code
Pingback: Mandelbrot Set Explorer | Science and Code